Ejemplos de Función Secante

Matemáticas → Anál. Matemático → Función → Secante

Definición de Función Secante:

La Función Secante es aquella función trigonométrica que tiene la siguiente fórmula:

f(x) = sec x

Recordemos que la secante de un ángulo α (sec α) es la razón entre la hipotenusa y el cateto contiguo (o adyacente) al ángulo. Es la razón recíproca al coseno:

Representación Gráfica de la Función Secante:

La función secante tiene la siguiente representación gráfica:

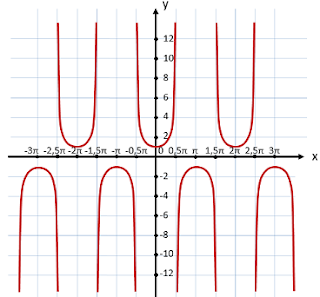
La función secante tiene las siguientes propiedades:

• Es una función continua  en todo x excepto en los siguientes puntos: π·k + π/2 (donde k es un número entero)
• Toma los siguientes valores: (-∞, -1] ∪ [1, +∞)
• Tiene un periodo de 2π radianes, es decir, se repite cada 2π radianes
• Es una función par, es decir: sec -x = sec x
• No corta al eje horizontal (eje x) en ningún punto

Otros Tipos de Funciones:

• Función Acotada: función f tal que para cualquier valor de x, -m ≤ f(x) ≤ m 
• Función Afín: f(x) = mx + n (donde m y n ≠ 0)
• Función Algebraica: expresiones algebraicas (suma, resta, multiplicación...) de números y variables
• Función Compleja: f: S → C, donde C es el conjunto de los números complejos
• Función Continua: función cuya curva está formada por un trazo continuo sin saltos
• Función Constante: f(x) = m, donde m es constante
• Función Creciente: función f tal que f(x₁) ≤ f(x₂) para cualquier par de puntos x₁ < x₂
• Función Cuadrática:  f(x) = ax² + bx + c
• Función Cúbica: f(x) = ax³ + bx² + cx + d
• Función Decreciente: función f tal que f(x₁) ≥ f(x₂) para cualquier par de puntos x₁ > x₂
• Función Discontinua: función cuya curva está formada por un trazo con saltos o roto en su trazo
• Función Escalar: f: Rⁿ → R 
• Función Explícita: y = f(x)
• Función Exponencial: f(x) = e^x
• Función Identidad: f(x) = x
• Función Impar: f(-x) = -f(x)
• Función Implícita: y ≠ f(x)
• Función Inversa: f^-1(x)
• Función Lineal: f(x) = mx
• Función Logarítmica: f(x) = log_a x
• Función Par: f(x) = f(-x)
• Función Parte Entera: f(x) = E(x)
• Función Periódica: f(x) = f(x + T)
• Función Polinómica: f(x) = a_nxⁿ + a_n−1xⁿ⁻¹ + ... + a₂x² + a₁x + a₀
• Función Potencial: f(x) = x^a
• Función Primitiva: F(x)
• Función Racional: f(x) = P(x) / Q(x) donde P y Q son dos polinomios
• Función Real: f: R → R 
• Función Trigonométrica: incluye en su fórmula alguna razón trigonométrica (seno, coseno, tangente...)
• Función Valor Absoluto: f(x) = |P(x)| donde P es un polinomio
• Función Vectorial: f: Rⁿ → R^m

versión 1 (01/05/2017)