Matemáticas → Anál. Matemático → Función → Discontinuidad Evitable
Definición de Discontinuidad Evitable:
Una Discontinuidad en una Función consiste en la rotura de la continuidad de dicha función en alguno de sus puntos.
Una Discontinuidad Evitable en un punto x0 de una función es aquella discontinuidad en la cual la función tiene límite en ese punto pero es distinto del valor de la función para ese punto o directamente no existe función para dicho punto.
Es decir, o bien:
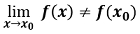
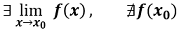
Ejemplos de Discontinuidad Evitable:
Ejemplo 1: tomemos la siguiente función
f(x) = {1 si x < 1, x si x > 1}
En dicha función, la función tiene una discontinuidad en el punto x = 1 ya que:
Una Discontinuidad Evitable en un punto x0 de una función es aquella discontinuidad en la cual la función tiene límite en ese punto pero es distinto del valor de la función para ese punto o directamente no existe función para dicho punto.
Es decir, o bien:
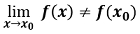
o bien:
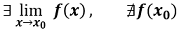
Ejemplos de Discontinuidad Evitable:
Ejemplo 1: tomemos la siguiente función
f(x) = {1 si x < 1, x si x > 1}
En dicha función, la función tiene una discontinuidad en el punto x = 1 ya que:
- Existe el límite de la función para el punto x = 1
- No existe función para dicho punto ya que no está definida
f(x) = {1 si x < 1, x si x ≥ 1}
Ejemplo 2: tomemos la siguiente función
f(x) = {1 si x < 1, 5 si x = 1, x si x > 1}
Ejemplo 2: tomemos la siguiente función
f(x) = {1 si x < 1, 5 si x = 1, x si x > 1}
En este caso, la función tiene límite para el punto x = 1 y vale 1 pero es diferente al valor de dicha función en ese punto ya que f(1) es igual a 5 y por lo tanto distinto.
¿Eres capaz de encontrar más ejemplos? Te animamos a compartirlos abajo en los comentarios.
¿Eres capaz de encontrar más ejemplos? Te animamos a compartirlos abajo en los comentarios.
Tipos de Funciones:
Veamos los diferentes tipos de funciones:
Veamos los diferentes tipos de funciones:
- Función Real: f: R → R
- Función Compleja: f: C → C
- Función Escalar: f: Rn → R
- Función Vectorial: f: Rn → Rm
- Función Identidad
- Función Inyectiva
- Función Biyectiva
- Función Sobreyectiva
- Función Inversa
- Función Continua
- Función Constante
- Función Compuesta
- ...

No hay comentarios :
Publicar un comentario