Matemáticas → Anál. Matemático → Función → Discontinuidad
Definición de Discontinuidad:
Una Discontinuidad en una Función consiste en la rotura de la continuidad de dicha función en alguno de sus puntos.
Intuitivamente, podemos entender una discontinuidad como aquella región de la gráfica que no se puede dibujar sin levantar el lápiz del papel.
En el anterior ejemplo se observa una discontinuidad en el punto x = 1 de la función.
Tipos de Discontinuidad:
Veamos a continuación cuáles son los principales tipos de discontinuidades de una función:
Intuitivamente, podemos entender una discontinuidad como aquella región de la gráfica que no se puede dibujar sin levantar el lápiz del papel.
En el anterior ejemplo se observa una discontinuidad en el punto x = 1 de la función.
Tipos de Discontinuidad:
- Discontinuidad Evitable:
En una función se produce una discontinuidad evitable en el punto x0 si la función tiene límite en ese punto pero es distinto del valor de la función para ese punto o no existe.
Es decir:
o
- Discontinuidad Esencial o Discontinuidad No Evitable:
Las discontinuidades esenciales o discontinuidades no evitables pueden ser de primera o segunda especie.
- Discontinuidad de Primera Especie:
Los límites laterales de la función en un punto son distintos o uno de ellos diverge. Puede ser a su vez de varios tipos.
- Discontinuidad de Salto Finito
- Discontinuidad de Salto Infinito
- Discontinuidad Asintótica
- Discontinuidad de Segunda Especie:
La función no existe o no tiene límite en uno o ambos lados del punto de discontinuidad
¿Eres capaz de encontrar más ejemplos? Te animamos a compartirlos abajo en los comentarios.
Tipos de Funciones:
Veamos los diferentes tipos de funciones:
Veamos los diferentes tipos de funciones:
- Función Real: f: R → R
- Función Compleja: f: C → C
- Función Escalar: f: Rn → R
- Función Vectorial: f: Rn → Rm
- Función Identidad
- Función Inyectiva
- Función Biyectiva
- Función Sobreyectiva
- Función Inversa
- Función Continua
- Función Constante
- Función Compuesta
- ...

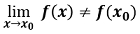
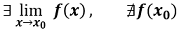
No hay comentarios :
Publicar un comentario